Stormwater Best Management Practices in an Ultra-Urban Setting: Selection and Monitoring
4.6 Monitoring Program Evaluation Phase
The monitoring program culminates in the evaluation phase. In this phase, possible data analysis techniques for answering management questions identified in the planning phase are reviewed and an appropriate data analysis methodology is selected. A good understanding of the data limitations is essential for selecting an appropriate data analysis methodology. Any conclusions or inferences should include a statement on the associated degree of confidence. Important considerations in assessing the degree of confidence associated with any conclusions are (1) the representativeness of the data of short- and long-term variabilities in the hydrologic regime and (2) the sufficiency of the data to answer management questions to the desired degree of confidence.
Understanding the representativeness of samples is crucial to allow meaningful conclusions. Consider, for example, a situation where the mean annual loading of a pollutant from a watershed is to be estimated before initiating BMP implementation. Data are available on event mean concentrations for a range of flows sampled over a 3-year period. Before beginning any data analysis, it is advisable to determine how representative the samples are of the range of conditions generating pollutant loadings in the watershed. Since the pollutant loadings are driven by rainfall, the range of conditions could be assessed by examining historical records of the amount, intensity, and duration of rainfall events. However, establishing the range of pollutant generating conditions based on these variables can be difficult. In addition, pollutant generation will also be impacted by antecedent moisture and land use conditions.
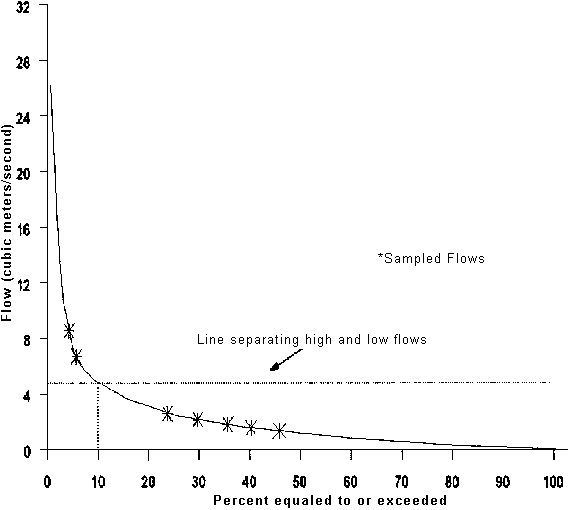
Another approach to assessing the range of conditions generating pollutant loadings is through flow duration curves, which are plots of daily discharge as a function of the percentage of time the discharge is exceeded. Flow duration curves represent the expected streamflow variability at a site and can be used as surrogates for the range of conditions generating pollutant loadings (Richards, 1988). Thus, to determine the representativeness of samples obtained during the monitoring period, the flows associated with each sample could be located on the flow duration curve (Figure 48). Runoff related flows are separated from low flows at some exceedence probability level, assumed to be 10 percent in the figure and indicated by a dashed line. This provides a compact pictorial summary of the data representativeness. The location of sampling points in Figure 48 suggest that relatively few samples were taken under high-flow conditions. If a large part of the variability in pollutant loadings is due to runoff events, this would indicate that any loading estimates derived from the current sample would have a high degree of uncertainty.
To determine whether the data are sufficient to answer management questions to the desired degree of confidence, an approach similar to the one outlined in the data collection protocols, in which the number of samples are estimated, can be employed. However, the population variance required to estimate the number of samples is now determined from data collected in the monitoring program, and is therefore more reliable.
Data analysis in a monitoring program may involve:
- Obtaining representative values for pollutant removal efficiencies based on concentration or total mass reduction.
- Using statistical inferential techniques to estimate parameters and test a hypothesis (e.g., is the effluent concentration less than the influent concentration at the 5 percent significance level?).
The use of inferential techniques in data analysis lends greater credibility to any statements about BMP effectiveness and allows the monitoring results to be used with greater confidence. However, the majority of studies in the past have based their conclusions on pollutant removal efficiency calculations and have not attempted to use inferential techniques in data analysis. This may be due to several reasons, including budgetary constraints and, in some cases, a reluctance on the part of investigators to interpret their results in probabilistic terms.
Pollutant Removal Efficiencies
The USEPA (1983b) proposed two basic methods for computing pollutant removal efficiency. The average event mean concentration efficiency ratio (Eemc) and summation of loads efficiency ratio (Esol), expressed as percentages, are computed as follows:
Eemc = (1 - AEMCout/AEMCin) × 100
Esol = (1 - SOLout/SOLin) × 100
where AEMC is the average event mean concentration, SOL is the summation of loads, and the subscripts "out" and "in" refer to outlet and inlet, respectively. Loads are computed as the product of event mean concentrations and the associated volume. It should be noted that while these efficiencies are defined using the average event mean concentration or the sums of loads for all monitored storms, similar efficiencies can be computed on an event-by-event basis. For example, individual storm removal efficiencies based on input and output event mean concentrations are often used to report maximum and minimum storm removal efficiencies.
Martin and Smoot (1986) have suggested an alternative method of computing pollutant removal efficiency based on a least-squares simple linear regression of loads (ROL). In this method, output loads are regressed against inlet loads with the slope of the regression line constrained to zero. The regression slope is regarded as the transport rate of the constituent through the BMP and one minus the regression slope is defined as the pollutant removal efficiency.
Data Requirements and Assumptions. Unlike the AEMC efficiency method, which gives equal weight, by averaging, to each storm event, the SOL and ROL efficiency methods require concomitant data for input and output storm loads. The AEMC and SOL methods assume that monitored storms are representative of normally occurring storms within the region being applied (Martin, 1988). These methods also assume that the inlet and outlet concentrations and loads are statistically significant for estimating percent removal (i.e., the equations are independent of the number of samples collected during a storm event). The SOL method further assumes that the samples collected were sufficient to represent all significant input and output loads. The ROL method assumes that the treatment efficiency is equivalent for any storms that are monitored (Martin, 1988).
General Results. Martin (1988) found that in general all three methods yield similar results, but that AEMC efficiencies produce the lowest values, ROL efficiencies yield the highest values, and SOL values lie between the two. However, in the case when there is a loss of runoff volume from inflow to outflow, the SOL and ROL methods will generally yield higher efficiencies. This occurs because any loss of runoff volume contributes to a reduction in the constituent load, but does not necessarily contribute to a reduction in constituent concentration (Martin, 1988). Martin (1988) found that the ROL efficiencies were slightly higher than the SOL efficiencies and attributed this fact to the zero-intercept constraint that is placed on the linear best fit regression line. By constraining the intercept to zero, the effect of small-load storms is minimized, thereby giving more weight to large-load storms. The box below provides an illustration of an urban detention system where pollutant removal efficiencies were calculated using all three methods.
Advantages and Disadvantages. The AEMC method is capable of providing information concerning the effect of a BMP on water quality by providing an average event mean concentration of constituents delivered to downstream receiving waters. However, because the AEMC method combines storm data to produce an event mean, the results of using this method may be somewhat biased (Martin, 1988). AEMCs do not show the range of possible values associated with the water quality variable, and they do not provide information about changes in concentrations associated with storm magnitude. The major advantage is that one sample is processed in the laboratory, thereby saving money and time associated with laboratory analyses.
|
Effectiveness of an Urban Runoff
Detention Pond-Wetlands System
The effectiveness of an urban detention system located in Orlando, Florida, for reducing constituent concentrations and loads transported by urban stormwater runoff was investigated (Martin, 1988). The study included measurement and sampling of runoff from 11 storms during a 2-year period. Discharge at the pond inlet was measured with an electromagnetic current meter mounted in the center of the inlet culvert. Discharge at the wetlands outlet was determined from the record of wetlands stage and a weir, calibrated using current-meter discharge measurements. The automatic sampling at the pond inlet was controlled by pond inlet velocity. The sampling at the outlet was controlled by the pond stage. Discrete sampling was used for six of the 11 storms. Four to six samples from as many as 24 that were collected during a single storm event were selected for laboratory analysis. It was assumed that constituent concentrations for periods between samples varied linearly between the selected samples. Composite sampling was used for the remaining five storms. One flow-weighted sample was composited using all of the samples collected during a single storm. The constituent loads were calculated as the product of the composite sample constituent concentration and the total volume of runoff. The event mean concentrations for the discretely sampled storms were calculated by dividing the constituent load by the cumulative discharge at each of the measuring points. Efficiency estimates for selected constituents for the detention pond using the AEMC, SOL, and ROL methods are shown below.
|
| |
Efficiency (%) |
| Constituent |
AEMC |
SOL |
ROL |
| TS |
10 |
16 |
22 |
| TP |
28 |
33 |
38 |
| Pb |
31 |
32 |
40 |
|
The SOL method provides a good measure of the overall efficiency of a BMP. The SOL method gives somewhat more weight to the large-load storms, but like the AEMC method, it does not provide information on individual storms (Martin, 1988). Laboratory time and cost are increased because individual samples have to be analyzed.
The ROL method provides not only a measure of the overall efficiency of a BMP, but also an indication of efficiency consistency (Martin, 1988). However, because the intercept is constrained at zero (i.e., zero input load = zero output load), the ROL method gives much more weight to larger storms (Martin, 1988). As with the SOL method, laboratory time and cost are increased because individual samples have to be analyzed. To allow comparison of results reported from different studies, it is important that pollutant removal efficiencies be computed in a consistent manner. In particular, it is difficult to compare results from studies that only report individual storm maximum and minimum removal efficiencies with studies that report removal efficiencies based on the sum of load observed for all monitored storms. Urbonas (1995) recommends that for consistency, the percent removal for any constituent should be calculated and reported for each monitored event using inflow and outflow loads. He further recommends that any summary report should include the mean of individual event percent removal rates and the coefficient of variation over the monitoring period.
Strecker (1995) points out that for BMPs where there is a permanent pool, computing pollutant removal effectiveness for individual storms may not be meaningful since the outflow may have no or only a limited relationship to the inflow. For these BMPs, it may be more appropriate to use total loads over the monitored period to compute removal efficiencies.
Statistical Inferential Techniques
The basic approach in any data analysis using statistical inference is to formulate a hypothesis. This is done by stating the null hypothesis and an alternative hypothesis. The null hypothesis is usually stated in a no-effect form (i.e., the effect being tested for is not present). The alternative hypothesis is simply a statement of what is true when the null hypothesis is rejected. The null hypothesis is tested by computing a test statistic from the available data. The alternative hypothesis is accepted when the significance level of a statistical test (also called the probability of a Type I error or p value) is less than a prespecified value. The Type I error or p value refers to the probability of rejecting the null hypothesis when it is actually true. Since hypothesis tests are based on inferences made from finite-sized samples drawn from a population, it is necessary to specify an acceptable Type I error rate. It is standard practice to have a Type I error rate of 5 percent (i.e.,when the achieved p value of a statistical test is less than 0.05, the result is regarded as significant and the null hypothesis is rejected).
The significance level of a statistical test is obtained by locating the test statistic in the assumed distribution of the statistic. Depending on how the alternative hypothesis is specified, the test may be described as one-tailed or two-tailed. In a one-tailed test, the alternative hypothesis is stated as an inequality (e.g., the parameter of interest is less than some prespecified value). In a two-tailed test, the alternative hypothesis is stated in a "not equal to" form (i.e., the parameter of interest may be less than or greater than some prespecified value). In a one-tailed test, the rejection region (values of the test statistic for which the null hypothesis will be rejected) lies on only one side of the test statistic distribution, whereas in a two-tailed test the rejection region lies on both sides of the test statistic distribution.
Statistical hypothesis tests usually require one or more assumptions about the data. Assumptions made by statistical tests should be clearly understood and every attempt made to verify whether they are valid. Two commonly required assumptions in statistical tests are normality and independence.
The normality assumption requires that the observed data be drawn from a normal (Gaussian) probability distribution. With few exceptions, statistical tests that require the normality assumption (called parametric tests) perform poorly when the underlying distribution is not normal. Since the normality assumption may be difficult to justify for many variables of interest, many authors have suggested that nonparametric (sometimes called distribution-free) statistical tests should be routinely used in the analysis of water quality data. The assumptions on underlying distributions required by nonparametric tests are usually far less stringent, and in some cases there may be no assumptions required. When the assumption of a normal distribution is difficult to verify (e.g., when there are missing data or when the sample size is very small), it is advantageous to employ nonparametric techniques.
The assumption of independence is crucial for both parametric and nonparametric tests. Independent observations (i.e., a random sample) ensure that information obtained from individual observations is maximized. In general, both parametric and nonparametric procedures are not robust to dependencies between data.
Before conducting any formal statistical tests, it is beneficial to conduct an exploratory data analysis using summary statistics and graphical representations of the data. Exploratory data analysis assists in developing a mental picture of the data and can be used to assess the validity of assumptions made in formal statistical tests.
Summary statistics can include measures of central tendency such as the mean and median, measures of dispersion such as variance and the inter-quartile range, and measures of association such as the correlation coefficient. Graphical representations can include histograms, box-and-whisker plots, ranked data (empirical distribution function) plots, and normal probability plots. Details on how to obtain summary statistics and graphical representations of data can be found in USEPA (1996).
Most statistical tests of interest in BMP evaluation are hypothesis tests about a single population (one-sample tests) or tests for comparing two populations (two-sample tests). In hypothesis tests about a single population, current conditions (e.g., current pollutant loads) are compared to a fixed threshold value (such as a regulatory standard or some other acceptable risk level). A hypothesis test for two populations generally involves a "before and after" comparison. For example, consider a situation where monitoring data are available for a number of years on instream constituent concentrations before and after BMP implementation. The data obtained before BMP implementation could be used in a one-tailed single-sample test to determine whether instream pollutant concentrations were higher than ambient values. Data obtained before and after BMP implementation could be used in a two-tailed two-sample test to determine whether there was a significant difference between the constituent concentrations before and after BMP implementation. If a significant difference were indicated by the test, an estimator for the difference could be obtained and confidence intervals for the estimator could be computed. The various steps involved in performing parametric and nonparametric one-sample and two-sample tests are presented in the boxes below.
Parametric Single-Sample Test
(one-sample t-test)
Assumptions
- Observations are independent
- Observations are drawn from a population that is approximately normal
Components
- Ho (null hypothesis): population mean (µ) is equal to some prespecified value (µo): µ = µo
- HA (alternative hypotheses):
- One-tailed test: µ < µo (or µ > µo)
- Two-tailed test: µ ≠ µo
- Test statistic (t) = (x - µo) ⁄ (S ⁄ √n) where x is the sample mean, S is the sample standard deviation, and √n is the number of observations
- Rejection region:
- one-tailed test :
t < - t1 - α, n - 1 (for HA : µ < µo)
t > - t1 - α, n - 1 (for HA : µ > µo)
- two-tailed test :
t < - t1 - α ⁄ 2, n - 1 or t > - t1 - α ⁄ 2, n - 1
where α is the significance level of the test.
Note: The subscripts for critical t values in the rejection region refer to the probability of non-exceedence and degrees of freedom, respectively. For example, t1 - α, n - 1 is the value of the variate that has a non-exceedence probability of (1 - α) on a t distribution with n - 1 degrees of freedom. |
Parametric Two-Sample Test
(two-sample t-test)
Assumptions
- Independent observations are drawn from two populations. Each observation is independent from other observations in the same population as well as all observations in the other population.
- Both populations sampled are approximately normal.
- The variance of both populations is the same.
Components
- Ho (null hypothesis): The difference in population means (µ1 - µ2) is equal to some prespecified value (Do):
µ1 - µ2 = Do (Do is commonly zero in which case Ho : µ1 = µ2).
- HA (alternative hypotheses):
- One-tailed test: (µ1 - µ2) < Do (or (µ1 - µ2) > Do)
- Two-tailed test: (µ1 - µ2) ≠ Do
- Test statistic
(t) = [(x1 - x2) - Do] ⁄ √[SP2(1 ⁄ n1+1 ⁄ n2)]
where x1 and x2 are the sample means, and n1 and n2 are the number of observations from the first and second populations, is the pooled variance estimate computed as:
SP2 = [(n1 - 1)S21+(n2 - 1)S21] ⁄ [n1+n2 - 2]
where S21 and S22 are sample variances from the first and second populations.
- Rejection region:
- One-tailed test :
t < t1 - α,n1+n2 - 2
t > t1 - α,n1+n2 - 2
- Two-tailed test :
t < t1 - α,n1+n2 - 2 or
t > t1 - α,n1+n2 - 2
where α is the significance level of the test.
|
Nonparametric Single-Sample Test
(Wilcoxon signed rank test)
Assumptions
- Observations are independent.
- Observations are drawn from a population that has a symmetric frequency distribution curve.
Components
- Ho (null hypothesis): population mean (µ) is equal to some prespecified value (µo):
- HA (alternative hypothesis):
- One-tailed test: µ < µo (or µ > µo)
- Two-tailed test: µ ≠ µo
- Test statistic:
To compute the test statistics follow these steps:
- Subtract µo from each observation to obtain deviations. If a deviation is zero, delete the observation from the analysis and reduce the sample size accordingly.
- Assign ranks based on ordering the absolute value of the deviations (i.e., the magnitude of differences ignoring the sign) from smallest to largest (rank 1 is assigned to the smallest value). If there are ties, the average of the ranks which would have been assigned to the tied observations is assigned to each tied observation.
- Assign signed ranks to each observation. The signed rank for an observation is positive if the deviation is positive and negative if the deviation is negative.
- Calculate the following statistics:
T+ = sum of positive signed ranks
T– = absolute value of sum of signed ranks
T = smaller of T+ and T–.
- Rejection region:
- One-tailed test :
T– ≤ To ( HA: µ < µo)
T+ ≤ To ( HA: µ > µo)
- Two-tailed test :
T ≤ To
where To is obtained from a table of critical values of the test statistic in the Wilcoxon signed rank test (e.g., McClave and Dietrich, 1985, page 793) at a given level of significance (a) for the number of untied pairs.
When the sample size is larger than about 25, the test statistic can be estimated from
z = [R - n(n+1) ⁄ 4] ⁄ √{[n(n+1)2n+1] ⁄ 24}
where z is a standard normal variate and R = T– for a left-tailed test (HA: µ < µo), R = T+ for a right-tailed test ( HA: µ > µo), and R = T for a two-tailed test. The corresponding rejection regions are:
- z < - zα (HA: µ < µo)
- z > zα ( HA: µ > µo)
- z < - zα or z > zα ⁄ 2 ( HA: µ ≠ µo)
|
Nonparametric Two-Sample Test
(Wilcoxon rank sum test)
Assumptions
- Independent observations are drawn from two populations. Each observation is independent from other observations in the same population as well as other observations in the other population.
- The populations have the same dispersion (variance).
Components
- Ho (null hypothesis): two sampled populations (A and B) have identical probability distributions.
- HA (alternative hypothesis): One-tailed test: The probability distribution of A is shifted to the right of that for B (or A is shifted to the left of B) Two-tailed test: The probability distribution of A is shifted to the right or to the left of B.
- Test statistic:
To compute the test statistics follow these steps:
- Pool all observations from both samples and rank from the smallest (rank 1) to the largest.
- Calculate the sum of ranks of the data from population A (TA) and population B (TB). The rank sum test statistic is the rank sum associated with the sample with fewer measurements. If the sample sizes are equal, either rank sum may be used.
-
Rejection region:
If TA is selected as the test statistic, then for
- One-tailed test :
TA ≥ Tu (for HA: distribution of A is shifted to the right of B)
TA ≥ T1 (for HA: distribution of A is shifted to the left of B)
- Two-tailed test :
TA ≥ Tu or TA ≥ T1
where TU and TL are obtained from a table of critical values of the test statistic in the Wilcoxon rank sum test (e.g., McClave and Dietrich, 1985, page 792) at a given level of significance (a) and the appropriate sample sizes (nA and nB).
When the sample size is larger than 10, the test statistic can be estimated from
z = [TA - nA(nA+nB+1) ⁄ 2] ⁄ √[nAnB(nA+nB+1) ⁄ 12]
where z is a standard normal variate. The corresponding rejection regions are:
- z > zα (HA : distribution of A shifted to the right of B)
- z < - zα (HA : distribution of A shifted to the left of B)
- z < - zα ⁄ 2 or zα ⁄ 2 (HA : distribution of A shifted to the right or left of B)
|
In some situations, data may be obtained from two populations where the assumption of independence between the samples is not valid. If the data can be paired in some manner, it is more appropriate to make inferences about the difference between the two populations using the paired data set and analyze the data as a single sample. Pairing is accomplished by subtracting observations in one sample from the equivalent observation in the other sample. An example of a paired sample analysis is presented below.
Paired Sample Analysis
Influent and effluent concentrations of zinc for a sand filter were measured for 14 storms. The data are provided below:
| Storm |
Inflow concentration (mg/L) |
Outflow concentration(mg/L) |
| 1 |
0.066 |
0.309 |
| 2 |
0.134 |
0.432 |
| 3 |
0.887 |
0.067 |
| 4 |
0.362 |
0.048 |
| 5 |
0.504 |
0.059 |
| 6 |
0.679 |
0.055 |
| 7 |
0.191 |
0.021 |
| 8 |
0.177 |
0.032 |
| 9 |
0.115 |
0.018 |
| 10 |
0.196 |
0.015 |
| 11 |
0.085 |
0.014 |
| 12 |
0.095 |
0.017 |
| 13 |
0.117 |
0.016 |
| 14 |
0.128 |
0.015 |
Determine if a significant reduction in zinc concentration is indicated at the 0.05 level, and obtain an estimator for the reduction in concentration.
The inflow and outflow concentrations cannot be assumed to be independent, so a two-sample test would be inappropriate and a paired sample analysis should therefore be employed. Paired differences are obtained by subtracting the outflow concentrations from the inflow concentrations for each storm. The null hypothesis (H0) and alternative hypotheses (HA) are specified below:
H0: µd = 0
HA: md > 0
where µd is the mean of the paired differences. If the paired differences are assumed to follow a normal distribution, a t-statistic can be computed for a one-sample t test:
t = (x - µd) ⁄ (s ⁄ √n) = (0.187 - 0) ⁄ (0.297 ⁄ √14) = 2.357
where x is the mean of observed differences, s is the standard deviation of observed differences, and n is the number of observations.
We reject the null hypothesis if the t statistic is greater than the critical value (t0.05,13). From a t table, we note that the critical t value is 1.771. Therefore, the null hypothesis is rejected at the 0.05 level. Further examination of the t table reveals that the achieved level of significance is between 0.01 and 0.05 (0.01 < p < 0.05). An estimator for the reduction in concentration is simply the mean of the paired differences (x), and is equal to 0.187 mg/L. If the assumption of a normal distribution is not felt to be valid, the equivalent nonparametric test (Wilcoxon signed rank one-sample test) can be conducted on the paired differences. Computing the sum of the ranks with a negative sign and comparing to the critical values for the Wilcoxon signed rank test statistic results in an achieved significance level of between 0.01 and 0.025 (0.01 < p < 0.025).
|
A number of considerations should be kept in mind when the monitoring data contain nondetects. If less than 15 percent of total samples are nondetects, they may be replaced by a small number (such as the detection limit divided by 2) and data analysis performed in the usual manner. However, when the sample data have between 15 and 50 percent nondetects, it is necessary to provide adjusted estimates of central tendency and dispersion that account for data below the detection limit. If the percentage of nondetects is between 50 and 90 percent, it may be necessary to perform hypothesis tests on a parameter that is some percentile greater than the percentage of nondetects. Tests are performed for proportions with the hypothesis written in terms of percentiles (e.g., the null hypothesis would be "the 75th percentile is less than or equal to some value"). It is difficult to make statistical inferences on data that have more than 90 percent nondetects. Table 26 summarizes procedures that should be employed when analyzing data with between 15 and 90 percent nondetects. Details on these procedures can be found in USEPA (1996).
Table 26. Data Analysis with Greater Than 15% Nondetects
| Percentage of Nondetects |
Suggested Procedure for Analysis |
| 15 - 50 |
Provide adjusted estimates of central tendency and dispersion that account for data below the detection limit |
| 50 - 90 |
Perform hypothesis tests on a parameter that is some percentile greater than the percentage of nondetects |
|
Reference Conditions
In an evaluation of a porous pavement method by Hogland et al. (1987), reductions in solids and metals were noted; however, there was an increase in the export of soluble forms of nitrogen. The increase in the concentration of nitrogen was linked to the location of the BMP in an old agricultural area. Prior fertilizer use had increased the naturally occurring amount of NO3, NO2, NH4, and even chloride in soil at the site. Decomposition of root masses after clearing had also likely increased the amount of NO3, NO2, and NH4 in soil. Large negative removals (exports) of nitrogen were measured during the course of this BMP evaluation.
|
Constituents such as nutrients and metals occur naturally in surface waters and represent the preexisting loadings from a BMP drainage area. In addition, prior agricultural land uses or localized increases in atmospheric deposition due to the proximity of incinerators or industrial smokestacks may have resulted in elevated concentrations of some constituents at a monitoring site. All these inputs are in addition to inputs that result from urban land uses like highways. The incidence and extent of these prior conditions affect the evaluation of BMP removal efficiencies based on a measurement of the differences in mass loading between the inlet and outlet of a structure.
Prior to the second year of a multi-year monitoring program, or following a point when sufficient data has been collected for the development of a correlation matrix, prioritization of the collection of constituent data may be justified (USDA, 1993). Constituents that have been monitored and which show low coefficients of variation may be candidates for a reduced sampling effort.
|
Constituent Prioritization
An evaluation of the suspended sediment and nutrient removal efficiency of a sand filter BMP has been ongoing for a six months. Samples from fifteen events have been collected to date. Resources are available to continue the collection of samples another six months, but the budget for laboratory analysis has almost been used up. The constituents monitored to date include:
- total suspended solids (TSS)
- volatile suspended solids (VSS)
- total phosphorus (TP)
- ortho-phosphate (OP)
- total Kjeldahal nitrogen (TKN)
- ammonia nitrogen (NH3)
- nitrate nitrogen (NO3)
Based on 1997 costs the submission of a water sample for these analyses would cost $230 per sample. Which parameters could be dropped to allow the budget for laboratory analysis to last until the end of the monitoring project?
A correlation analysis based on the data collected to date resulted in the following matrices:
| |
TSS |
|
| VSS |
0.764 |
|
| |
TKN |
NO3 |
| NH3 |
0.836 |
0.2
81 |
| NO3 |
- 0.057 |
|
| |
TP |
|
| OP |
0.915 |
|
Correlations between TSS and VSS, TKN and NH3, TP and OP are significant and very high. Adequate monitoring could be achieved by continuing to monitor only TSS, TKN, TP and NO3. This would reduce the cost per sample to $125, reducing the analytical cost by almost half (USDA, 1993).
Consider, for example, the loadings of a metal constituent such as lead, which may have a naturally occurring background EMC concentration of 10µg/L in surface flow from a BMP drainage area. Localized deposition from an incinerator might have elevated this EMC concentration to 25 µg/L while prior application of municipal sludge to agricultural land that has now been converted to an urban land use might have increased this EMC to 30 µg/L. Stormwater inputs from the current urban land use result in a final EMC of 50 µg/L. Monitoring results from a BMP evaluation show a load reduction from an EMC of 50 to 25 µg/L or 50 percent removal efficiency or 125 percent of the loading, which can be directly attributed to inputs from the current urban land use.
|
References
APHA. 1995. Standard Methods for the Examination of Water and Wastewater. 19th ed. American Public Health Association (APHA), Washington, DC.
Barrett, M.E., R.D. Zuber, E.R. Collins III, J.F. Malina, Jr., R.J. Charbeneau, and G.H. Ward. 1995. A Review and Evaluation of Literature Pertaining to the Quantity and Control of Pollution from Highway Runoff and Construction. 2nd ed. Technical Report CRWR 239. Center for Research in Water Resources, the University of Texas at Austin.
Bellinger, W.Y. 1980. Runoff Monitoring. Federal Highway Administration, Region 15, Demonstration Projects Division, Arlington, VA.
Bos, M.G. 1988. Discharge Measurement Structures. 3rd rev. ed. International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands.
Brookes, A. 1988. Channelized Rivers: Perspectives for Environmental Management. John Wiley and Sons, New York, NY.
Coffey, S.W., J. Spooner, and M.D. Smolen. 1993. The Nonpoint Source Manager's Guide to Water Quality and Land Treatment Monitoring. NCSU Water Quality Group, Department of Biological and Agricultural Engineering, Raleigh, NC.
D'Andrea, M., D.E. Maunder, and W. Snodgrass. 1993. Characterization of Stormwater and Combined Sewer Overflows in Metropolitan Toronto. Proceedings of the Stormwater Management and Combined Sewer Control Technology Transfer Conference. January 19-20, 1993, Etobicoke, ON.
Driscoll, E., and P. Mangarella. 1990. Urban Targeting and BMP Selection. Prepared by Woodward-Clyde Consultants, Oakland, CA, for U.S. Environmental Protection Agency, Washington, DC.
Driscoll, E.D., P.E. Shelley, and E.W. Strecker. 1990. Pollutant Loadings and Impacts from Highway Stormwater Runoff. Volume III: Analytical Investigations and Research Report. FHWA-RD-88-008. Prepared by Woodward-Clyde Consultants, Oakland, CA, for Federal Highway Administration, Washington, DC.
FIASP ( Federal Inter-Agency Sedimentation Project of the Inter-Agency Committee on Water Resources). 1966. Instruments and Reports for Fluvial Sediments Investigations St. Anthony Falls Hydraulic Lab., MN.
Gilbert, R.O. 1987. Statistical Methods for Environmental Pollution Monitoring. Van Nostrand Reinhold, New York, NY.
Glick, R.H., M.L. Wolfe, and T.L. Thurow. 1993. Effectiveness of Native Species Buffer Zones for Nonstructural Treatment of Urban Runoff. Texas Water Resources Institute, College Station, TX.
Hale, W.E. 1972. Sample Size Determination for the Lognormal Distribution. Atmos. Environ.,6:419 - 422.
Hogland, W., J. Niemczynowice, and T. Wahlan. 1987. The Unit Superstructure during the Construction Period. The Science of the Total Environment (59):411 - 424.
Horner, R.R., and C.R. Horner. 1995. Design, Construction, and Evaluation of a Sand Filter Stormwater Treatment System. Part II. Performance Monitoring. Report to Alaska Marine Lines, Seattle, WA.
Keith, L.H. 1991. Environmental Sampling and Analysis: A Practical Guide. Lewis Publishers, Chelsea, MI.
Khan, Z., C. Thrush, P. Cohen, L. Kulzer, R. Franklin, D. Field, J. Koon, and R. Horner. 1992. Biofiltration Swale Performance, Recommendations, and Design Considerations. Municipality of Metropolitan Seattle, Water Pollution Control Department, Seattle, WA.
Maestri, B., M.E. Dorman, and J. Hartigan. 1988. Managing Pollution from Highway Stormwater Runoff. Transportation Research Record 1166, Issues in Environmental Analysis. Transportation Research Board, Washington, DC.
Marsalek, J. 1973. Instrumentation for Field Studies of Urban Runoff. Environment Canada. Environmental Protection Service. Training and Technology Transfer Division (Water), Ottawa, ON.
Martin, E.H. 1988. Effectiveness of an Urban Runoff Detention Pond - Wetlands System. Journal of Environmental Engineering 114(4):810.
Martin, E.H., and J.L. Smoot. 1986. Constituent - Load Changes in Urban Stormwater Runoff Routed Through a Detention Pond - Wetlands System in Central Florida. U.S. Geological Survey Water Resources Investigations Report 85-4310. Tallahassee, FL.
McClave, J.T., and F.H. Dietrich. 1985. Statistics. Dellen Publishing Company, San Francisco, CA.
McCrea, R.C., and J.D. Fischer. 1993. Quality Assurance and Control Considerations for the ISOMET Stream Sampler. Environment Canada, Ecosystem Health Division, Burlington, ON.
Nunnally, N.R., and E.A. Keller. 1979. Use of Fluvial Processes to Minimize Adverse Effects of Stream Channelization. Water Resources Research Institute, UNC, NC, Report No. 144.
Ongley, E., and Blachford, D. 1982. Applications of Continuous - Flow Centrifugation to Contaminant Analysis of Suspended Sediment in Fluvial Systems. Environ. Technol. Lett. 3:219-288.
Richards, R.P. 1988. Approaches to Characterizing Substance Loads and Flows from Great Lakes Tributaries. International Joint Commission, Windsor, ON.
Sanders, T.G., R.C. Ward, J.C. Loftis, T.D. Steele, D.D. Adrian, and V. Yevjevich. 1983. Design of Networks for Monitoring of Water Quality. Water Resources Publications, Littleton, CO.
Savile, H. 1980. CCIW/NWRI Operating and Maintenance Manual for Westphalia Clarifier. National Water Research Institute, Canada Centre for Inland Waters, Burlington, ON.
Strecker, E. 1995. Constituents and Methods for Assessing BMPs. In Proceedings of the Engineering Foundation Conference on Stormwater Related Monitoring Needs. ASCE, New York, NY.
USDA. 1993. Water Quality Monitoring.U.S. Department of Agriculture (USDA), Soil Conservation Service, Washington, DC.
USEPA. 1982. Handbook for Sampling and Preservation of Water and Wastewater. EPA-600/4-28-029. U.S. Environmental Protection Agency (USEPA), Environmental Monitoring and Support Laboratory, Cincinnati, OH.
USEPA. 1983a. Final Report of the Nationwide Urban Runoff Program. U.S. Environmental Protection Agency, Water Planning Division, Washington, DC.
USEPA. 1983b. Methods for Chemical Analysis of Water and Wastes. EPA 600/4-79-020. U.S. Environmental Protection Agency, Environmental Monitoring Support Laboratory, Cincinnati, OH.
USEPA. 1991. Monitoring Guidance for the National Estuary Program. EPA 503/8-91-002. U.S. Environmental Protection Agency, Office of Wetlands, Oceans, and Watersheds, Washington, DC.
USEPA. 1992. NPDES Storm Water Sampling Guidance Document. EPA 833-B-92-001. U.S. Environmental Protection Agency, Office of Water, Washington, DC.
USEPA. 1993. Guidance Specifying Management Measures for Sources of Nonpoint Pollution in Coastal Waters. EPA-840-B-92-002. U.S. Environmental Protection Agency, Office of Water, Washington, DC.
USEPA. 1994a. EPA Requirements for Quality Assurance Project Plans for Environmental Data Operations. EPA QA/R-5. U.S. Environmental Protection Agency, Quality Assurance Management Staff, Washington, DC.
USEPA. 1994b. Guidance for the Data Quality Objectives Process. EPA QA/G-4. EPA/600/R-96/055. U.S. Environmental Protection Agency, Office of Research and Development, Washington, DC.
USEPA. 1995. Nonpoint Source Monitoring and Evaluation Guide. U.S. Environmental Protection Agency, Office of Water, Washington, DC. Final Review Draft, September.
USEPA. 1995. Guidance for the Preparation of Standard Operating Procedures (SOPs) for Quality - Related Documents. EPA QA/G-6. U.S. Environmental Protection Agency, Office of Research and Development, Washington, DC.
USEPA. 1996. Guidance for Data Quality Assessment - Practical Methods for Data Analysis. EPA QA/G-9. U.S. Environmental Protection Agency, Office of Research and Development, Washington, DC.
USGS. 1977. Chapter 5: Chemical and Physical Quality of Water and Sediment. National Handbook of Recommended Methods for Water - Data Acquisition. U.S. Geological Survey (USGS), Office Water Data Coord., Reston, VA.
USGS. 1982. National Handbook of Recommended Methods for Water - Data Acquisition. U.S. Geological Survey, Reston, VA.
Urbonas, B.R. 1995. Parameters to Report with BMP Monitoring Data. In Stormwater NPDES Related Monitoring Needs, ed. H.C.Torno, pp. 306 - 328. American Society of Civil Engineers, New York, NY.
Young, G.K, S. Stein, P. Cole, T. Kammer, F. Graziano, and F. Bank. 1996. Evaluation and Management of Highway Runoff Water Quality. Federal Highway Administration, Washington, DC.
Yu, S.L., S.L. Barnes, and V.W. Gerde. 1993. Testing of Best Management Practices for Controlling Highway Runoff. Virginia Department of Transportation, Report No. FHWA/VA-93-R16, Richmond, VA.
Yu, S.L., and R.J. Kaighn. 1995. The Control of Pollution in Highway Runoff Through Biofiltration. Volume II: Testing of Roadside Vegetation. Virginia Department of Transportation, Report No. FHWA/VA-95-R29, Richmond, VA.
Yu, S.L., R.J. Kaighn, and S.L. Liao. 1994. Testing of Best Management Practices for Controlling Highway Runoff, Phase II. Virginia Department of Transportation, Report No. FHWA/VA-94-R21, Richmond, VA.
|

